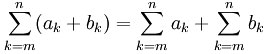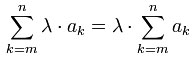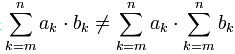2.3.1 Trigonometric and Logarithmic Functions

VCmaster is proficient in all mathematical functions of the scientific calculator including all parenthesis levels and exponentiations.  The function descriptions are either entered directly or called up via the menu.

When using the menu VCmaster assists by inserting predefined functions e.g. SIN(). The cursor is automatically positioned in the brackets for the function value to be entered, which can either be a numerical value or a variable. 
All functions can be linked, i.e. a function value can also contain a function call (for nesting: See examples). 

The VCmaster TechEditor can interpret super scripted characters so that the expression X2 , written with (ALT GR+2 ) is equivalent to the representation X2 (written with super scripted 2). X1/3 will also be correctly evaluated, rendering special exponential functions unnecessary. 

Naturally all current mathematical rules apply. If an equation is unsolvable, VCmaster shows a relevant error message. Calculation then continues with the number of decimal places specified. Meaning, if a higher calculation accuracy is required, the number of places after the decimal point has to be increased.

MENU:

 Calculate-Angular function/Logarithm

Examples

Trigonometric function:
Width b = 200. 00 mm
Angle α = 45. 00 °
Height h = b * SIN( α ) = 141. 42 mm

Exponentiation (automatic interpretation of superscripted fields):
χ = 1/(φ+(φ²-λ²)0,5) 0. 8083

Exponentiation (ALT GR+2 * or ALT GR+3 key * ):
Width b = 10. 00 mm
Height h = 20. 00 mm

I =
b * h3 / 12
6666.
67 mm4
Note: Depending on the specific charset

2.3.2 Logical functions

Functions such as ABS(), MAX(), MIN(), IF(), AND, OR are realized. Arguments are separated by semicolons.

The IF function consists of three elements: The condition, the formula or the value that is to be used if the condition is fulfilled, and the formula or the value that is relevant if the condition is not fulfilled.

In the IF function all common operators "=" , "≠" , ">" , "<" , “≥" and “≤"" are allowed. Text variables can be compared although only numerical values are allowed as a result.

The IF function is resolved from right to left. Hence, it makes sense to utilize brackets in operations.

Examples
IF function (read: if; then; else):
D = 55.00 mm
k = IF( D≤32; 1; 1 - 0.26*LOG(D/32))) = 0. 939

IF function (nested):
d = 20 cm
b = IF( d>25; 1;IF( d>17.5 ; 0.9 ; 0.75) ) = 0. 90

Example with text variables:
Steel = "S355"
Re = IF( Steel="S235" ; 235 ; 355 ) = 355. 00 N/mm2

Example with text variables:
FEd = 45.00 kN
FRd = 50.00 kN
Re = IF( FEd / FRd ≤ 1; "valid"; "invalid" ) = admissible
Re = IF( FEd / FRd ≤ 1; FEd / FRd ; "invalid" ) = 0,90
Exception: If an if () function, that usually returns a number, returns a text in case of an error, this variable will no longer be used for calculations.

Example showing different brackets (red) and the results:
A = 15
b = 30

IF( A < 10 AND B < 20 OR B > 25; 1; 0.80 ) = 1. 00
IF( (A < 10 AND B < 20) OR B > 25; 1; 0.80 ) = 1. 00
IF( A < 10 AND (B < 20 OR B > 25); 1; 0.80 ) = 0. 80

Examples of MIN()- / MAX() function:
F1 = 150 N
F2 = 200 N

FMAX = MAX( F1; F2 ) = 200. 00 N
  MIN (F1; F2 * 0.50 ) = 100. 00 N
Note: The IF() call can be hidden in the printout. For details, see Chapter 2.9

2.3.3 Defining Options


The OPT() function provides predefined options for selection::

Variable X = OPT( "Opt1"; "Opt2"; ... )

Selecting an option is done with a double-click, analogous to the SEL() function. A default of "NULL" defines an empty default (e.g. for result output).

NULL as a variable value: Defines an empty variable. See the examples as well. A variable of the form Var = "NULL" is suppressed in result output. Using the expression Var = NULL (without quotation marks) is permitted.

Note: he OPT() call can be hidden on print. See Chapter 2.10.3.


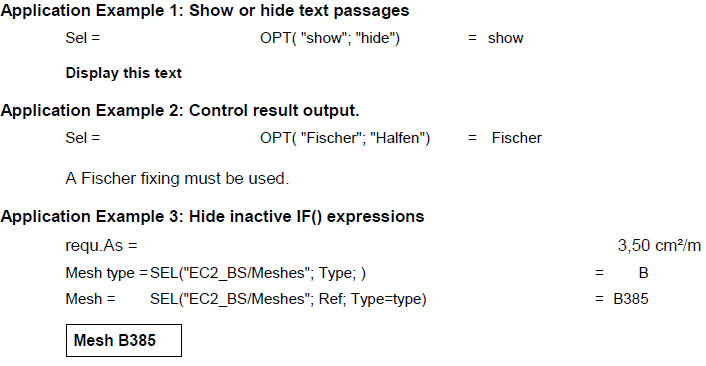
Application Example 1: Show or hide text passages
Display it:

Hidden:



Application Example 2: Control result output
Input:

Output: A Fischer fixing must be used.


Application Example 3: Hide inactive IF() expressions
Additional reinforcement required:


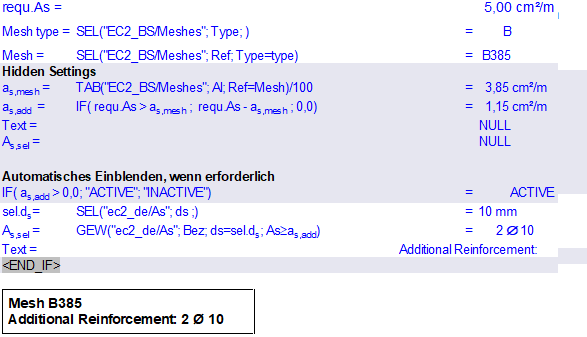
Without additional reinforcement:


The output is fully automatic and adapts depending on requ.As.

Display of the above examples in the output (PDF or print)
The gray-shaded lines are, of course, hidden in the output. It would then look like this:



MENÜ:

 Calculation – Conditions and Options

2.3.4 Rounding functions

ROUND Rounds a number to a specified number of digits (half to even)
ROUNDDOWN Rounds a number down, toward zero
ROUNDUP Rounds a number up, away from zero
MROUND Rounds a number up, to the desired multiple
   
Syntax ROUND( number ; num_digits )
ROUNDDOWN( number ; num_digits )
ROUNDUP( number ; num_digits )
MROUND( number ; multiple )
number: The number that you want to round
num_digits: The number of digits to which you want to round the number argument
multiple: The multiple to which you want to round number
   
Examples
ROUND(2.15 ; 1) Rounds 2.15 to one decimal place 2.2
ROUND(2.149 ; 1) Rounds 2.149 to one decimal place 2.1
ROUND(21.5 ; -1) Rounds 21.5 to one decimal place to the left of the decimal point 20
ROUND(626.3; -3) Rounds 626.3 to the nearest multiple of 1000 1000
     
ROUNDDOWN(2.15 ; 1) Rounds 2.15 downs to one decimal place 2.1
ROUNDDOWN(76.9 ; 0) Rounds 76.9 down to zero decimal places 76
ROUNDDOWN(31415.9; -2) Rounds 31415.9 down to 2 decimal places to the left of the
decimal point		 31400
     
ROUNDUP(2.15 ; 1) Rounds 2.15 up to one decimal place 2.2
ROUNDUP(76.9 ; 0) Rounds 76.9 up to zero decimal places 77
ROUNDUP(31415.9; -2) Rounds 31415.9 up to 2 decimal places to the left of the
decimal point		 31500
     
MROUND(2.5 ; 1) Rounds 2.5 up to nearest multiple of 1 3
MROUND(1.5 ; 0.1) Rounds 1.5 up to the nearest multiple of 0.1 1.5
MROUND(0.234 ; 0.01) Rounds 0.234 up to the nearest multiple of 0.01 0.24

EVEN Rounds a number up to the nearest even integer
ODD Rounds a number up to the nearest odd integer
   
Syntax EVEN( number )
ODD( number )
number: The value to round  
   
Examples
EVEN( 1.5 ) Rounds 1.5 to the nearest even integer 2
EVEN( 3 ) Rounds 3 to the nearest even integer 4
     
ODD( 1.5 ) Rounds 1.5 up to the nearest odd integer 3
ODD( 3 ) Rounds 3 up to the nearest odd integer 3

2.3.5 Summation and Absolute value function

Both functions are entered in the graphic formula editor.
The entry of a total corresponds with the mathematical rules.

Note: The index must be identical with the mathematical rules.

Rules:




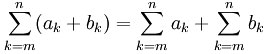
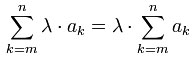
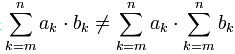Example:


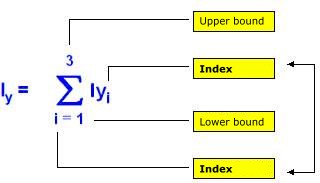
The example shows the following summation:

Iy = Iy1+ Iy2 + Iy3

2.3.6 Conversion of Units of Measurements

On generating a formula, every variable can be allocated the unit of measurement expected by the formula. Alternatively the shortcut CTRL + # is available. This function calls for the use of a graphic formula, which will be generated automatically after text input. The target unit of measurement is hidden during this operation. It can be modified later in the Formula Editor.


The fact that formulae are always calculated correctly regardless of the underlying variable is a major advantage of allocating target units of measurements.

Using B= 8,00 dm as shown in the example would generate the identical value for the area. Using target units of measurements, errors while copying formulae and templates are avoided. If a unit of measurement can not be converted, an error message is shown instead. For validation purposes the converted value can be displayed. Working with target units of measurements is especially recommended in countries working with various units and not only with SI-units. VCmaster is able of working with and converting e.g. British Units.

MENU:

 Calculate- Other functions-Target unit